What is the layered structure and ion distribution?-Tycorun Batteries

main content:

1. Layered structure Li-Mn-O

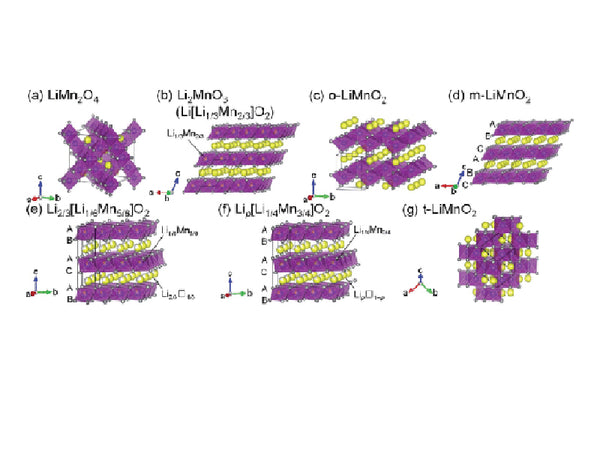
Li₂MnO₃ is alternately filled in tightly packed oxygen planes by lithium-manganese-lithium (the ratio of lithium to manganese is 2:1). The tightly packed oxygen array deviates slightly from the ideal cubic tightly packed. The structure of Li₂MnO₃ is very similar to layered LiCoO₂ and LiNiO₂, which can be regarded as [Li]_3a(Li_0.33Mn_0.67)_3bO₂, where 3a and 3b refer to the octahedral position in the triangular lattice. The arrangement of cations in Li₂MnO₃ reduces the symmetry of the crystal from the typical cubic symmetry of the rock salt structure to monoclinic symmetry.

There are 9 clearly distinguishable peaks on the Raman scattering spectrum of monoclinic Li₂MnO₃, which are located at 248cm^-1, 308cm^-1, 332cm^-1, 369cm^-1, 413cm^-1, 438cm^-1, 493cm^-1, 568cm^-1 and 612cm^-1. Compared with spinel LiMn₂O₄, its spectral peak shifts to a lower energy direction, which is mainly caused by the difference in the chemical bonding environment between the two.

Figure 1 is an X-ray diffraction pattern of Li₂MnO₃ with rock salt structure and spinel compounds LiMn₂O₄ and Li₄Mn₅O₁₂. It can be seen from this figure that the diffraction patterns of these several compounds are very similar. It's just that Li₂MnO₃(135) and (2▔06) superimposed on the Bragg peak and (060) peak appear in the powder diffraction pattern with 2θ values of 64.6° and 65.2° respectively, while spinel LiMn₂O₄ is in the 2θ range of 64°~66° There is only one (440) surface diffraction peak.

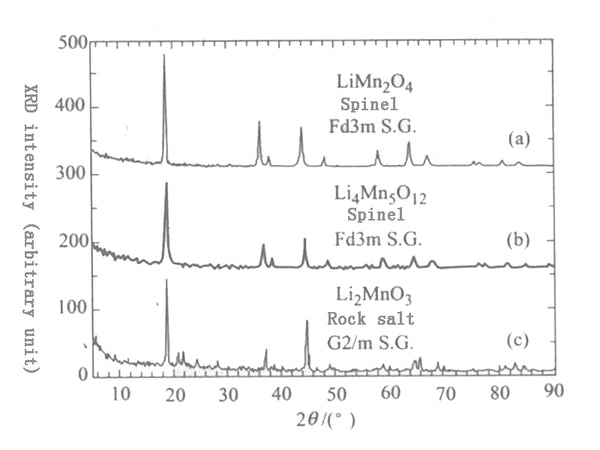
Figure 1 X-ray powder diffraction patterns of several Li-Mn-O compounds
(A) Spinel LiMn₂O₄; (b) Spinel Li₄Mn₅O₁₂;
(C) Rock salt Li₂MnO₃

Figure 2 shows the X-ray powder diffraction patterns of several Li-Mn-O materials such as spinel LiMn₂O₄, tetragonal Li₂Mn₂O₄, monoclinic LiMnO₂ and orthogonal LiMnO₂. It can be seen that the patterns of monoclinic layered LiMnO₂ and tetragonal spinel Li₂Mn₂O₄ are very similar, and it is difficult to distinguish the two by X-ray diffraction alone. This is mainly due to the severe Jahn-Teller effect of Mn³⁺, which reduces the symmetry of spinel lithium manganese oxide, which makes lithiated spinel Li₂[Mn³⁺]₂O₄ a tetragonal spinel of the I4_I/amd space group structure. The cation order in the tetragonal spinel structure is very similar to that in monoclinic layered LiMnO₂.

Figure 2 X-ray powder diffraction pattern of several Li-Mn-O compounds. 11 (a) Spinel LiMn₂O₄; (b) tetragonal Li₂Mn₂O₄; n i (c) monoclinic LiMnO₂; (d) orthogonal LiMnO₂

In monoclinic LiMnO₂, Li⁺ and Mn³⁺ are in the 2d position in the C2/m space group, while the oxygen anion is in the 4i position. Group theory calculations show that monoclinic LiMnO₂ has 3 Raman activity peaks and 6 infrared activity peaks, while the number of peaks observed in the experiment is higher than the theoretical prediction value. Three main Raman peaks of monoclinic LiMnO₂ were observed, located at 419cm^-1, 479cm^-1 and 605cm^-1, as shown in Figure 3(b). Three weak Raman peaks were detected at 575 (shoulder peak) cm^-1, 358cm^-1 and 286cm^-1. Compared with spinel LiMn₂O₄, its spectral peak shifts to a lower energy direction. Therefore, it is easy to distinguish the spinel Li₂Mn₂O₄ from monoclinic LiMnO₂ with only four spectral peaks in the range of 200~650cm^-1 by using Raman spectroscopy. For lithium manganese oxides with similar structures, Raman spectroscopy is an effective means to distinguish them.

Figure 3 Raman spectra of several Li-Mn-O compounds
(A) Li₂MnO₃; (b) monoclinic LiMnO₂;
(C) Li_0.33MnO₂; (d) Orthogonal LiMnO₂

2. Ion distributed

The prerequisite for the design of functional materials is to first determine the microstructure of the required material, and to study the way the atoms of the material are arranged in space, that is, the distribution of ions.

1) LiCr_xMn_2-xO_4-yA_y ion distribution and capacity calculation
The battery capacity (C) refers to the amount of electricity that can be obtained from the battery under certain discharge conditions. The theoretical capacity of the battery is calculated according to Faraday's law based on the mass of the active material, that is, the mass of the substance participating in the reaction on the electrode is proportional to the amount of electricity passed. The calculation formula is as follows:
C=6.023×10²³×1.6022×10^-19n×(m/FW)÷3600=26.8n(m/FW)

In the formula, m is the mass of the fully reacted active material; FW is the molecular weight of the active material; n is the number of electrons gained and lost during the flow reaction. It can be seen from the above formula that when the amount of active material in the battery is determined, its theoretical capacity is inversely proportional to the molecular weight of the active material, and proportional to the number of electrons gained and lost during the flow reaction.

For the spinel lithium manganese oxide cathode material, the molecular weight FW is almost a certain value, and the number of electrons gained and lost during the flow reaction has also been fixed to 1. For the stoichiometric spinel LiMn₂O₄, its ion distribution can be expressed as: [Li]_8a[Mn(Ⅲ)_pMn(IV)_q]_16dO₄. Li⁺ is located at the 8a position, Mn(Ⅲ) and Mn(IV) each account for half, located at the 16d position, and O^2－ is located at the 32e position. The calculation formula of its theoretical capacity is:
C=26.8×10³p/180.81(mA·h/g)